Formally verified Neural CBF in stochastic environment
Learning a formally verified CBF in stochastic environment
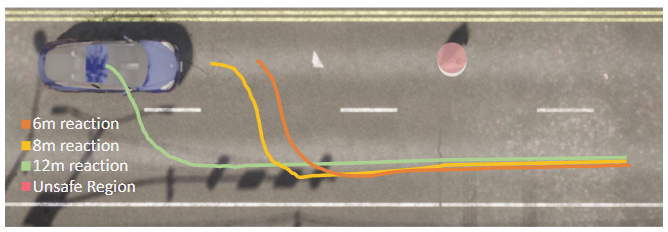
Safety is a fundamental requirement of control systems. Control Barrier Functions (CBFs) are proposed to ensure the safety of the control system by constructing safety filters or synthesizing control inputs. However, the safety guarantee and performance of safe controllers rely on the construction of valid CBFs. Inspired by universal approximatability, CBFs are represented by neural networks, known as neural CBFs (NCBFs). This paper presents an algorithm for synthesizing formally verified continuous-time neural Control Barrier Functions in stochastic environments in a single step. The proposed training process ensures efficacy across the entire state space with only a finite number of data points by constructing a sample-based learning framework for Stochastic Neural CBFs (SNCBFs). Our methodology eliminates the need for post hoc verification by enforcing Lipschitz bounds on the neural network, its Jacobian, and Hessian terms. We demonstrate the effectiveness of our approach through case studies on the inverted pendulum system and obstacle avoidance in autonomous driving, showcasing larger safe regions compared to baseline methods.
CP-NCBF: A Conformal Prediction-based Approach to Synthesize Verified Neural Control Barrier Functions
Control Barrier Functions (CBFs) are a practical approach for designing safety-critical controllers, but constructing them for arbitrary nonlinear dynamical systems remains a challenge. Recent efforts have explored learningbased methods, such as neural CBFs (NCBFs), to address this issue. However, ensuring the validity of NCBFs is difficult due to potential learning errors. In this letter, we propose a novel framework that leverages split-conformal prediction to generate formally verified neural CBFs with probabilistic guarantees based on a user-defined error rate, referred to as CP-NCBF. Unlike existing methods that impose Lipschitz constraints on neural CBF—leading to scalability limitations and overly conservative safe sets—our approach is sampleefficient, scalable, and results in less restrictive safety regions. We validate our framework through case studies on obstacle avoidance in autonomous driving and geo-fencing of aerial vehicles, demonstrating its ability to generate larger and less conservative safe sets compared to conventional techniques.
Neural Control Barrier Functions from Physics Informed Neural Networks
As autonomous systems become increasingly prevalent in daily life, ensuring their safety is paramount. Control Barrier Functions (CBFs) have emerged as an effective tool for guaranteeing safety; however, manually designing them for specific applications remains a significant challenge. With the advent of deep learning techniques, recent research has explored synthesizing CBFs using neural networks-commonly referred to as neural CBFs. This paper introduces a novel class of neural CBFs that leverages a physics-inspired neural network framework by incorporating Zubov’s Partial Differential Equation (PDE) within the context of safety. This approach provides a scalable methodology for synthesizing neural CBFs applicable to high-dimensional systems. Furthermore, by utilizing reciprocal CBFs instead of zeroing CBFs, the proposed framework allows for the specification of flexible, user-defined safe regions. To validate the effectiveness of the approach, we present case studies on three different systems: an inverted pendulum, autonomous ground navigation, and aerial navigation in obstacle-laden environments.
Citation
@article{tayal2024learning,
title={Learning a Formally Verified Control Barrier Function in Stochastic Environment},
author={Tayal, Manan and Zhang, Hongchao and Jagtap, Pushpak and Clark, Andrew and Kolathaya, Shishir},
journal={arXiv preprint arXiv:2403.19332},
year={2024}
}
@misc{tayal2025cpncbfconformalpredictionbasedapproach,
title={CP-NCBF: A Conformal Prediction-based Approach to Synthesize Verified Neural Control Barrier Functions},
author={Manan Tayal and Aditya Singh and Pushpak Jagtap and Shishir Kolathaya},
year={2025},
eprint={2503.17395},
archivePrefix={arXiv},
primaryClass={eess.SY},
url={https://arxiv.org/abs/2503.17395},
}
@misc{agrawal2025neuralcontrolbarrierfunctions,
title={Neural Control Barrier Functions from Physics Informed Neural Networks},
author={Shreenabh Agrawal and Manan Tayal and Aditya Singh and Shishir Kolathaya},
year={2025},
eprint={2504.11045},
archivePrefix={arXiv},
primaryClass={cs.RO},
url={https://arxiv.org/abs/2504.11045},
}
Related Papers
|
2024 December |
Learning a Formally Verified Control Barrier Function in Stochastic Environment
Conference on Decision and Control (CDC) 2024, Milan, Italy |
|
2025 March |
CP-NCBF: A Conformal Prediction-based Approach to Synthesize Verified Neural Control Barrier Functions
Pre-print |
|
2025 April |
Neural Control Barrier Functions from Physics Informed Neural Networks
Pre-print |
People
Manan Tayal
Pushpak Jagtap
Andrew Clark
